Analyzing Coefficients - V2
Contents
Analyzing Coefficients - V2#
RENAME: we started to analyze the coefficents in lesson 01-v2. Consider a new name for this like "iterating on our coefficients" or "thoughtful selection of coefficients",etc
Lesson Objectives#
By the end of this lesson, students will be able to:
Extract and visualize coefficients in more helpful formats.
Interpret coefficients for raw data vs scaled data.
Use coefficient values to inform modeling choices (for insights).
Encode nominal categories as ordinal (based on the target)
Determine which version of the coefficients would be best for extracting insights and recommendations for a stakeholder.
Our Previous Results#
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
## Reviewing the options used
pd.set_option('display.max_columns',100)
pd.set_option('display.max_rows',100)
pd.set_option('display.float_format', lambda x: f"{x:,.2f}")
## Customization Options
plt.style.use(['fivethirtyeight','seaborn-talk'])
mpl.rcParams['figure.facecolor']='white'
## additional required imports
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.compose import make_column_transformer, make_column_selector, ColumnTransformer
from sklearn.pipeline import make_pipeline, Pipeline
from sklearn import metrics
import joblib
Code/Model From Previous Lesson#
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
## Customization Options
plt.style.use(['fivethirtyeight','seaborn-talk'])
mpl.rcParams['figure.facecolor']='white'
## additional required imports
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.compose import make_column_transformer, make_column_selector, ColumnTransformer
from sklearn.pipeline import make_pipeline, Pipeline
from sklearn import metrics
SEED = 321
np.random.seed(SEED)
## Load in the King's County housing dataset and display the head and info
url = "https://docs.google.com/spreadsheets/d/e/2PACX-1vS6xDKNpWkBBdhZSqepy48bXo55QnRv1Xy6tXTKYzZLMPjZozMfYhHQjAcC8uj9hQ/pub?output=xlsx"
df = pd.read_excel(url,sheet_name='student-mat')
df.info()
df.head()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 395 entries, 0 to 394
Data columns (total 33 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 school 395 non-null object
1 sex 395 non-null object
2 age 395 non-null float64
3 address 395 non-null object
4 famsize 395 non-null object
5 Pstatus 395 non-null object
6 Medu 395 non-null float64
7 Fedu 395 non-null float64
8 Mjob 395 non-null object
9 Fjob 395 non-null object
10 reason 395 non-null object
11 guardian 395 non-null object
12 traveltime 395 non-null float64
13 studytime 395 non-null float64
14 failures 395 non-null float64
15 schoolsup 395 non-null object
16 famsup 395 non-null object
17 paid 395 non-null object
18 activities 395 non-null object
19 nursery 395 non-null object
20 higher 395 non-null object
21 internet 395 non-null object
22 romantic 395 non-null object
23 famrel 395 non-null float64
24 freetime 395 non-null float64
25 goout 395 non-null float64
26 Dalc 395 non-null float64
27 Walc 395 non-null float64
28 health 395 non-null float64
29 absences 395 non-null float64
30 G1 395 non-null float64
31 G2 395 non-null float64
32 G3 395 non-null float64
dtypes: float64(16), object(17)
memory usage: 102.0+ KB
| school | sex | age | address | famsize | Pstatus | Medu | Fedu | Mjob | Fjob | reason | guardian | traveltime | studytime | failures | schoolsup | famsup | paid | activities | nursery | higher | internet | romantic | famrel | freetime | goout | Dalc | Walc | health | absences | G1 | G2 | G3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | GP | F | 18.00 | U | GT3 | A | 4.00 | 4.00 | at_home | teacher | course | mother | 2.00 | 2.00 | 0.00 | yes | no | no | no | yes | yes | no | no | 4.00 | 3.00 | 4.00 | 1.00 | 1.00 | 3.00 | 6.00 | 5.00 | 6.00 | 6.00 |
| 1 | GP | F | 17.00 | U | GT3 | T | 1.00 | 1.00 | at_home | other | course | father | 1.00 | 2.00 | 0.00 | no | yes | no | no | no | yes | yes | no | 5.00 | 3.00 | 3.00 | 1.00 | 1.00 | 3.00 | 4.00 | 5.00 | 5.00 | 6.00 |
| 2 | GP | F | 15.00 | U | LE3 | T | 1.00 | 1.00 | at_home | other | other | mother | 1.00 | 2.00 | 3.00 | yes | no | yes | no | yes | yes | yes | no | 4.00 | 3.00 | 2.00 | 2.00 | 3.00 | 3.00 | 10.00 | 7.00 | 8.00 | 10.00 |
| 3 | GP | F | 15.00 | U | GT3 | T | 4.00 | 2.00 | health | services | home | mother | 1.00 | 3.00 | 0.00 | no | yes | yes | yes | yes | yes | yes | yes | 3.00 | 2.00 | 2.00 | 1.00 | 1.00 | 5.00 | 2.00 | 15.00 | 14.00 | 15.00 |
| 4 | GP | F | 16.00 | U | GT3 | T | 3.00 | 3.00 | other | other | home | father | 1.00 | 2.00 | 0.00 | no | yes | yes | no | yes | yes | no | no | 4.00 | 3.00 | 2.00 | 1.00 | 2.00 | 5.00 | 4.00 | 6.00 | 10.00 | 10.00 |
# ## Load in the King's County housing dataset and display the head and info
# df = pd.read_csv("https://docs.google.com/spreadsheets/d/e/2PACX-1vSEZQEzxja7Hmj5tr5nc52QqBvFQdCAGb52e1FRK1PDT2_TQrS6rY_TR9tjZjKaMbCy1m5217sVmI5q/pub?output=csv")
# ## Dropping some features for time
# df = df.drop(columns=['date'])
# ## Make the house ids the index
# df = df.set_index('id')
# ## drop lat/long
# df = df.drop(columns=['lat','long'])
# ## Treating zipcode as a category
# df['zipcode'] = df['zipcode'].astype(str)
# df.info()
# df.head()
# ### Train Test Split
## Make x and y variables
y = df['G3'].copy()
X = df.drop(columns=['G3']).copy()
## train-test-split with random state for reproducibility
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=SEED)
# ### Preprocessing + ColumnTransformer
## make categorical & numeric selectors
cat_sel = make_column_selector(dtype_include='object')
num_sel = make_column_selector(dtype_include='number')
## make pipelines for categorical vs numeric data
cat_pipe = make_pipeline(SimpleImputer(strategy='constant',
fill_value='MISSING'),
OneHotEncoder(drop='if_binary', sparse=False))
num_pipe = make_pipeline(SimpleImputer(strategy='mean'))
## make the preprocessing column transformer
preprocessor = make_column_transformer((num_pipe, num_sel),
(cat_pipe,cat_sel),
verbose_feature_names_out=False)
## fit column transformer and run get_feature_names_out
preprocessor.fit(X_train)
feature_names = preprocessor.get_feature_names_out()
X_train_df = pd.DataFrame(preprocessor.transform(X_train),
columns = feature_names, index = X_train.index)
X_test_df = pd.DataFrame(preprocessor.transform(X_test),
columns = feature_names, index = X_test.index)
X_test_df.head(3)
| age | Medu | Fedu | traveltime | studytime | failures | famrel | freetime | goout | Dalc | Walc | health | absences | G1 | G2 | school_MS | sex_M | address_U | famsize_LE3 | Pstatus_T | Mjob_at_home | Mjob_health | Mjob_other | Mjob_services | Mjob_teacher | Fjob_at_home | Fjob_health | Fjob_other | Fjob_services | Fjob_teacher | reason_course | reason_home | reason_other | reason_reputation | guardian_father | guardian_mother | guardian_other | schoolsup_yes | famsup_yes | paid_yes | activities_yes | nursery_yes | higher_yes | internet_yes | romantic_yes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 15.00 | 1.00 | 2.00 | 1.00 | 2.00 | 0.00 | 4.00 | 3.00 | 2.00 | 1.00 | 1.00 | 5.00 | 2.00 | 9.00 | 10.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 338 | 18.00 | 3.00 | 3.00 | 1.00 | 4.00 | 0.00 | 5.00 | 3.00 | 3.00 | 1.00 | 1.00 | 1.00 | 7.00 | 16.00 | 15.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 291 | 17.00 | 4.00 | 3.00 | 1.00 | 3.00 | 0.00 | 4.00 | 2.00 | 2.00 | 1.00 | 2.00 | 3.00 | 0.00 | 15.00 | 15.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
def evaluate_linreg(model, X_train,y_train, X_test,y_test, return_df=False,
get_coeffs=True, coeffs_name = "Coefficients"):
results = []
y_hat_train = model.predict(X_train)
r2_train = r2_score(y_train,y_hat_train)
rmse_train = mean_squared_error(y_train,y_hat_train, squared=False)
results.append({'Data':'Train', 'R^2':r2_train, "RMSE": rmse_train})
y_hat_test = model.predict(X_test)
r2_test = r2_score(y_test,y_hat_test)
rmse_test = mean_squared_error(y_test,y_hat_test, squared=False)
results.append({'Data':'Test', 'R^2':r2_test, "RMSE": rmse_test})
results_df = pd.DataFrame(results).round(3).set_index('Data')
results_df.loc['Delta'] = results_df.loc['Test'] - results_df.loc['Train']
results_df = results_df.T
print(results_df)
if get_coeffs:
coeffs = pd.Series(model.coef_, index= X_train.columns)
if model.intercept_!=0:
coeffs.loc['intercept'] = model.intercept_
coeffs.name = coeffs_name
return coeffs
from sklearn.linear_model import LinearRegression
## fitting a linear regression model
lin_reg = LinearRegression()
lin_reg.fit(X_train_df, y_train)
coeffs_orig = evaluate_linreg(lin_reg, X_train_df, y_train, X_test_df,y_test,
coeffs_name='Original')
coeffs_orig
Data Train Test Delta
R^2 0.85 0.81 -0.04
RMSE 1.83 1.85 0.02
age -0.22
Medu 0.29
Fedu -0.18
traveltime 0.19
studytime -0.22
failures -0.10
famrel 0.31
freetime 0.02
goout -0.02
Dalc -0.21
Walc 0.26
health 0.03
absences 0.05
G1 0.14
G2 0.99
school_MS 0.38
sex_M -0.01
address_U 0.15
famsize_LE3 0.01
Pstatus_T 0.38
Mjob_at_home -0.05
Mjob_health -0.02
Mjob_other 0.16
Mjob_services 0.12
Mjob_teacher -0.21
Fjob_at_home 0.33
Fjob_health 0.38
Fjob_other -0.11
Fjob_services -0.54
Fjob_teacher -0.05
reason_course -0.09
reason_home -0.42
reason_other 0.30
reason_reputation 0.21
guardian_father -0.20
guardian_mother 0.07
guardian_other 0.13
schoolsup_yes 0.34
famsup_yes 0.16
paid_yes 0.16
activities_yes -0.34
nursery_yes -0.21
higher_yes 0.82
internet_yes -0.09
romantic_yes -0.29
intercept -0.95
Name: Original, dtype: float64
Iterating On Our Model#
Removing the Intercept#
First, we can remove the intercept from our model, which will force the LinearRegression to explain all of the price without being free to calculate whatever intercept would help the model.
## fitting a linear regression model
lin_reg = LinearRegression(fit_intercept=False)
lin_reg.fit(X_train_df, y_train)
coeffs_no_int = evaluate_linreg(lin_reg, X_train_df, y_train, X_test_df,y_test,
coeffs_name='No Intercept')
coeffs_no_int.sort_values()
Data Train Test Delta
R^2 0.85 0.81 -0.04
RMSE 1.83 1.85 0.02
Fjob_services -0.73
reason_home -0.66
guardian_father -0.52
Mjob_teacher -0.40
activities_yes -0.34
reason_course -0.33
Fjob_other -0.31
romantic_yes -0.29
guardian_mother -0.25
Mjob_at_home -0.24
Fjob_teacher -0.24
age -0.22
studytime -0.22
Mjob_health -0.21
Dalc -0.21
nursery_yes -0.21
guardian_other -0.19
Fedu -0.18
failures -0.10
internet_yes -0.09
Mjob_services -0.07
Mjob_other -0.03
reason_reputation -0.03
goout -0.02
sex_M -0.01
famsize_LE3 0.01
freetime 0.02
health 0.03
absences 0.05
reason_other 0.06
Fjob_at_home 0.13
G1 0.14
address_U 0.15
famsup_yes 0.16
paid_yes 0.16
Fjob_health 0.18
traveltime 0.19
Walc 0.26
Medu 0.29
famrel 0.31
schoolsup_yes 0.34
school_MS 0.38
Pstatus_T 0.38
higher_yes 0.82
G2 0.99
Name: No Intercept, dtype: float64
To Intercept or Not To Intercept?#
compare = pd.concat([coeffs_orig, coeffs_no_int],axis=1)
compare = compare.sort_values('Original')
compare['Diff'] = compare['No Intercept'] - compare['Original']
compare
| Original | No Intercept | Diff | |
|---|---|---|---|
| intercept | -0.95 | NaN | NaN |
| Fjob_services | -0.54 | -0.73 | -0.19 |
| reason_home | -0.42 | -0.66 | -0.24 |
| activities_yes | -0.34 | -0.34 | 0.00 |
| romantic_yes | -0.29 | -0.29 | -0.00 |
| age | -0.22 | -0.22 | -0.00 |
| studytime | -0.22 | -0.22 | -0.00 |
| Dalc | -0.21 | -0.21 | 0.00 |
| nursery_yes | -0.21 | -0.21 | 0.00 |
| Mjob_teacher | -0.21 | -0.40 | -0.19 |
| guardian_father | -0.20 | -0.52 | -0.32 |
| Fedu | -0.18 | -0.18 | -0.00 |
| Fjob_other | -0.11 | -0.31 | -0.19 |
| failures | -0.10 | -0.10 | 0.00 |
| internet_yes | -0.09 | -0.09 | 0.00 |
| reason_course | -0.09 | -0.33 | -0.24 |
| Mjob_at_home | -0.05 | -0.24 | -0.19 |
| Fjob_teacher | -0.05 | -0.24 | -0.19 |
| Mjob_health | -0.02 | -0.21 | -0.19 |
| goout | -0.02 | -0.02 | 0.00 |
| sex_M | -0.01 | -0.01 | 0.00 |
| famsize_LE3 | 0.01 | 0.01 | -0.00 |
| freetime | 0.02 | 0.02 | -0.00 |
| health | 0.03 | 0.03 | 0.00 |
| absences | 0.05 | 0.05 | -0.00 |
| guardian_mother | 0.07 | -0.25 | -0.32 |
| Mjob_services | 0.12 | -0.07 | -0.19 |
| guardian_other | 0.13 | -0.19 | -0.32 |
| G1 | 0.14 | 0.14 | -0.00 |
| address_U | 0.15 | 0.15 | 0.00 |
| famsup_yes | 0.16 | 0.16 | -0.00 |
| paid_yes | 0.16 | 0.16 | 0.00 |
| Mjob_other | 0.16 | -0.03 | -0.19 |
| traveltime | 0.19 | 0.19 | 0.00 |
| reason_reputation | 0.21 | -0.03 | -0.24 |
| Walc | 0.26 | 0.26 | 0.00 |
| Medu | 0.29 | 0.29 | 0.00 |
| reason_other | 0.30 | 0.06 | -0.24 |
| famrel | 0.31 | 0.31 | -0.00 |
| Fjob_at_home | 0.33 | 0.13 | -0.19 |
| schoolsup_yes | 0.34 | 0.34 | 0.00 |
| Fjob_health | 0.38 | 0.18 | -0.19 |
| school_MS | 0.38 | 0.38 | 0.00 |
| Pstatus_T | 0.38 | 0.38 | -0.00 |
| higher_yes | 0.82 | 0.82 | -0.00 |
| G2 | 0.99 | 0.99 | -0.00 |
At this point, there is a valid argument for using either model as the basis for our stakeholder recommendations.
As long as you are comfortable explaining the intercept as the baseline house price (when all Xs are 0), then it is not difficult to express the findings to a stakeholder.
Let’s see if either version looks better when visualzied.
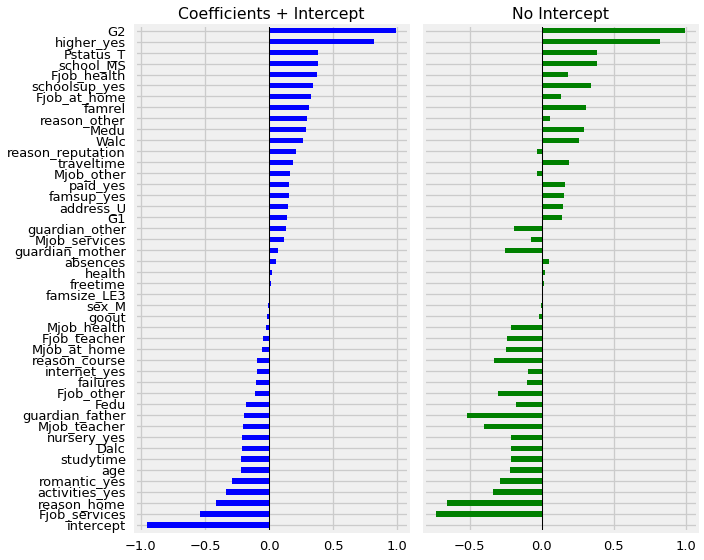
fig, axes = plt.subplots(ncols=2,figsize=(10,8),sharey=True)
compare['Original'].plot(kind='barh',color='blue',ax=axes[0],title='Coefficients + Intercept')
compare['No Intercept'].plot(kind='barh',color='green',ax=axes[1],title='No Intercept')
[ax.axvline(0,color='black',lw=1) for ax in axes]
fig.tight_layout()
compare['Diff'].plot(kind='barh',figsize=(4,10),color='red',title='Coeff Change W/out Intercept');
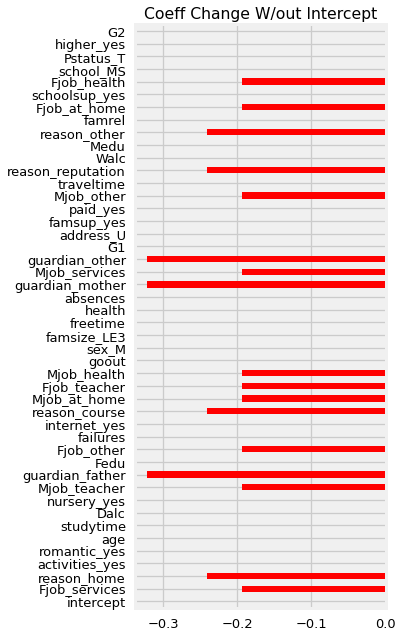
We can see that by removing the intercept from our model, which had a value of -.95, we have changed the value of several, but not all of the other coefficients.
Notice that, in this case, when our model removed a negative baseline value (the intercept), that many of the other coefficients became had a negative change. While this will not always be the case, it does demonstrate how our model has to change the coefficients values when it no longer can calculate a starting grade before factoring in the features.
Scaling Our Features#
Since we have entirely numeric features, we can simply scale our already-processed X_train/X_test variables by creating a new scaler.
Note: for more complicated datasets, we would want to create a new precprocessor where we add the scaler to the numeric pipeline.
# ### Preprocessing + ColumnTransformer
num_pipe_scale = make_pipeline(SimpleImputer(strategy='mean'), StandardScaler())
## make the preprocessing column transformer
preprocessor_scale = make_column_transformer((num_pipe_scale, num_sel),
(cat_pipe,cat_sel),
verbose_feature_names_out=False)
## fit column transformer and run get_feature_names_out
preprocessor_scale.fit(X_train)
feature_names = preprocessor_scale.get_feature_names_out()
X_train_scaled = pd.DataFrame(preprocessor_scale.transform(X_train),
columns = feature_names, index = X_train.index)
X_test_scaled = pd.DataFrame(preprocessor_scale.transform(X_test),
columns = feature_names, index = X_test.index)
X_test_scaled.head(3)
| age | Medu | Fedu | traveltime | studytime | failures | famrel | freetime | goout | Dalc | Walc | health | absences | G1 | G2 | school_MS | sex_M | address_U | famsize_LE3 | Pstatus_T | Mjob_at_home | Mjob_health | Mjob_other | Mjob_services | Mjob_teacher | Fjob_at_home | Fjob_health | Fjob_other | Fjob_services | Fjob_teacher | reason_course | reason_home | reason_other | reason_reputation | guardian_father | guardian_mother | guardian_other | schoolsup_yes | famsup_yes | paid_yes | activities_yes | nursery_yes | higher_yes | internet_yes | romantic_yes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | -1.30 | -1.61 | -0.49 | -0.65 | -0.01 | -0.44 | 0.07 | -0.17 | -0.94 | -0.52 | -0.98 | 1.03 | -0.47 | -0.56 | -0.17 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 338 | 1.01 | 0.22 | 0.43 | -0.65 | 2.38 | -0.44 | 1.18 | -0.17 | -0.05 | -0.52 | -0.98 | -1.81 | 0.17 | 1.53 | 1.13 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 291 | 0.24 | 1.14 | 0.43 | -0.65 | 1.18 | -0.44 | 0.07 | -1.16 | -0.94 | -0.52 | -0.22 | -0.39 | -0.72 | 1.23 | 1.13 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
## fitting a linear regression model
lin_reg = LinearRegression(fit_intercept=False)
lin_reg.fit(X_train_scaled, y_train)
coeffs_scaled = evaluate_linreg(lin_reg, X_train_scaled, y_train, X_test_scaled,y_test)
coeffs_scaled
Data Train Test Delta
R^2 0.85 0.81 -0.04
RMSE 1.83 1.85 0.02
age -0.29
Medu 0.32
Fedu -0.19
traveltime 0.14
studytime -0.18
failures -0.07
famrel 0.28
freetime 0.02
goout -0.02
Dalc -0.19
Walc 0.34
health 0.04
absences 0.42
G1 0.47
G2 3.81
school_MS 0.38
sex_M -0.01
address_U 0.15
famsize_LE3 0.01
Pstatus_T 0.38
Mjob_at_home 1.88
Mjob_health 1.91
Mjob_other 2.10
Mjob_services 2.05
Mjob_teacher 1.73
Fjob_at_home 2.26
Fjob_health 2.31
Fjob_other 1.82
Fjob_services 1.40
Fjob_teacher 1.89
reason_course 2.33
reason_home 2.00
reason_other 2.72
reason_reputation 2.63
guardian_father 3.03
guardian_mother 3.30
guardian_other 3.36
schoolsup_yes 0.34
famsup_yes 0.16
paid_yes 0.16
activities_yes -0.34
nursery_yes -0.21
higher_yes 0.82
internet_yes -0.09
romantic_yes -0.29
Name: Coefficients, dtype: float64
fig, ax = plt.subplots(figsize=(5,8))
coeffs_scaled.sort_values().plot(kind='barh')
# compare['Original'].plot(kind='barh',color='blue',ax=axes[0],title='Coefficients + Intercept')
# compare['No Intercept'].plot(kind='barh',color='green',ax=axes[1],title='No Intercept')
ax.axvline(0,color='black',lw=1)
<matplotlib.lines.Line2D at 0x2811f8160>
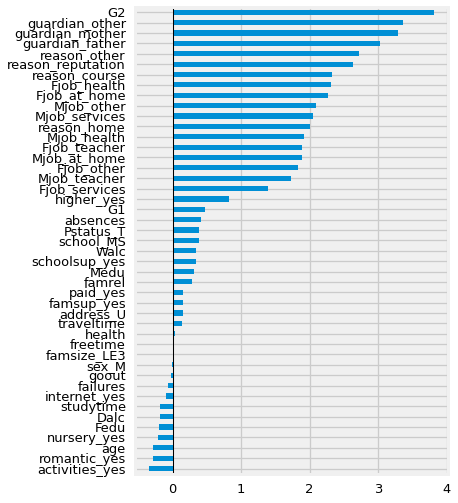
📌 TO DO#
visualize and discuss the scaled coefficients
select scaled vs not scaled
Revisiting Our Business Case#
Thus far, we have done all of our modeling under the assumption that we want to predict how well current students will do in their final year.
However, the stakeholder likely cares more about identifying how students will perform at very beginning of their Year 1.
Let’s keep this in mind and remove any features that we would not have known when the student was at the beginning of Year 1.
Modeling - For New Students#
We must remove:
G1: We wouldn’t know year 1 grades yet.
G2: We wouldn’t know year 1 grades yet.
We should probably remove:
paid: We would not know if students paid for extra classes in the subject yet.
Though we may be able to find out if they are WILLING to pay for extra classes.
activities: We would not know if the student was involved in extracurriculars at this school yet.
Though we may be able to ask students if they INTEND to be involved in activities.
We may want to remove:
absences:
We wouldn’t have absences from the current school, though we likely could get absences from their previous school.
Dalc: Work day alcohol consumption. Hopefully, the students who have not entered high school yet will not already be consuming alcohol.
Walc: weekend alcohol consumption. Hopefully, the students who have not entered high school yet will not already be consuming alcohol.
As you can see, some of the features are obviously inappropriate to include, but many of them are a bit more ambiguous. - Always think of your stakeholder’s goals/problem statement when deciding what features to include in your model/analysis.
When in doubt, contact and ask your stakeholder about the choice(s) you are considering!
DECIDE IF USING SCALED#
Unsaled#
## remove cols that MUST be removed.
df_mvp = df.drop(columns=['G1','G2'])
# ### Train Test Split
## Make x and y variables
y = df_mvp['G3'].copy()
X = df_mvp.drop(columns=['G3']).copy()
## train-test-split with random state for reproducibility
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=SEED)
## fit column transformer and run get_feature_names_out
preprocessor.fit(X_train)
feature_names = preprocessor.get_feature_names_out()
X_train_df = pd.DataFrame(preprocessor.transform(X_train),
columns = feature_names, index = X_train.index)
X_test_df = pd.DataFrame(preprocessor.transform(X_test),
columns = feature_names, index = X_test.index)
X_test_df.head(3)
| age | Medu | Fedu | traveltime | studytime | failures | famrel | freetime | goout | Dalc | Walc | health | absences | school_MS | sex_M | address_U | famsize_LE3 | Pstatus_T | Mjob_at_home | Mjob_health | Mjob_other | Mjob_services | Mjob_teacher | Fjob_at_home | Fjob_health | Fjob_other | Fjob_services | Fjob_teacher | reason_course | reason_home | reason_other | reason_reputation | guardian_father | guardian_mother | guardian_other | schoolsup_yes | famsup_yes | paid_yes | activities_yes | nursery_yes | higher_yes | internet_yes | romantic_yes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 15.00 | 1.00 | 2.00 | 1.00 | 2.00 | 0.00 | 4.00 | 3.00 | 2.00 | 1.00 | 1.00 | 5.00 | 2.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 338 | 18.00 | 3.00 | 3.00 | 1.00 | 4.00 | 0.00 | 5.00 | 3.00 | 3.00 | 1.00 | 1.00 | 1.00 | 7.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 291 | 17.00 | 4.00 | 3.00 | 1.00 | 3.00 | 0.00 | 4.00 | 2.00 | 2.00 | 1.00 | 2.00 | 3.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
## fitting a linear regression model
lin_reg = LinearRegression(fit_intercept=False)
lin_reg.fit(X_train_df, y_train)
coeffs_mvp = evaluate_linreg(lin_reg, X_train_df, y_train, X_test_df,y_test)
coeffs_mvp
Data Train Test Delta
R^2 0.30 0.04 -0.26
RMSE 3.91 4.12 0.21
age -0.34
Medu 0.58
Fedu -0.06
traveltime -0.13
studytime 0.29
failures -1.79
famrel 0.12
freetime 0.27
goout -0.70
Dalc -0.33
Walc 0.36
health -0.21
absences 0.05
school_MS 0.61
sex_M 1.00
address_U 0.60
famsize_LE3 0.29
Pstatus_T -0.12
Mjob_at_home 2.75
Mjob_health 4.74
Mjob_other 2.74
Mjob_services 3.59
Mjob_teacher 1.42
Fjob_at_home 3.21
Fjob_health 3.34
Fjob_other 2.23
Fjob_services 2.39
Fjob_teacher 4.06
reason_course 2.82
reason_home 3.60
reason_other 4.56
reason_reputation 4.26
guardian_father 4.43
guardian_mother 4.88
guardian_other 5.93
schoolsup_yes -1.08
famsup_yes -1.07
paid_yes 0.41
activities_yes 0.06
nursery_yes -0.13
higher_yes 1.38
internet_yes 0.76
romantic_yes -1.39
Name: Coefficients, dtype: float64
As we can see above, NOT including the grade from year 2 dramatically hurts our model’s ability to predict the final grade.
Scaled#
## fit column transformer and run get_feature_names_out
preprocessor_scale.fit(X_train)
feature_names = preprocessor_scale.get_feature_names_out()
X_train_scaled = pd.DataFrame(preprocessor_scale.transform(X_train),
columns = feature_names, index = X_train.index)
X_test_scaled = pd.DataFrame(preprocessor_scale.transform(X_test),
columns = feature_names, index = X_test.index)
X_test_df.head(3)
| age | Medu | Fedu | traveltime | studytime | failures | famrel | freetime | goout | Dalc | Walc | health | absences | school_MS | sex_M | address_U | famsize_LE3 | Pstatus_T | Mjob_at_home | Mjob_health | Mjob_other | Mjob_services | Mjob_teacher | Fjob_at_home | Fjob_health | Fjob_other | Fjob_services | Fjob_teacher | reason_course | reason_home | reason_other | reason_reputation | guardian_father | guardian_mother | guardian_other | schoolsup_yes | famsup_yes | paid_yes | activities_yes | nursery_yes | higher_yes | internet_yes | romantic_yes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 15.00 | 1.00 | 2.00 | 1.00 | 2.00 | 0.00 | 4.00 | 3.00 | 2.00 | 1.00 | 1.00 | 5.00 | 2.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 338 | 18.00 | 3.00 | 3.00 | 1.00 | 4.00 | 0.00 | 5.00 | 3.00 | 3.00 | 1.00 | 1.00 | 1.00 | 7.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 291 | 17.00 | 4.00 | 3.00 | 1.00 | 3.00 | 0.00 | 4.00 | 2.00 | 2.00 | 1.00 | 2.00 | 3.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
## fitting a linear regression model
lin_reg = LinearRegression(fit_intercept=False)
lin_reg.fit(X_train_scaled, y_train)
coeffs_mvp_scaled = evaluate_linreg(lin_reg, X_train_scaled, y_train,
X_test_scaled,y_test,
coeffs_name="Scaled Coefficients")
coeffs_mvp_scaled
Data Train Test Delta
R^2 0.30 0.04 -0.26
RMSE 3.91 4.12 0.21
age -0.44
Medu 0.63
Fedu -0.06
traveltime -0.09
studytime 0.24
failures -1.29
famrel 0.11
freetime 0.27
goout -0.78
Dalc -0.29
Walc 0.47
health -0.30
absences 0.38
school_MS 0.61
sex_M 1.00
address_U 0.60
famsize_LE3 0.29
Pstatus_T -0.12
Mjob_at_home 1.65
Mjob_health 3.64
Mjob_other 1.64
Mjob_services 2.49
Mjob_teacher 0.33
Fjob_at_home 2.12
Fjob_health 2.24
Fjob_other 1.13
Fjob_services 1.30
Fjob_teacher 2.97
reason_course 1.45
reason_home 2.22
reason_other 3.19
reason_reputation 2.89
guardian_father 2.61
guardian_mother 3.05
guardian_other 4.10
schoolsup_yes -1.08
famsup_yes -1.07
paid_yes 0.41
activities_yes 0.06
nursery_yes -0.13
higher_yes 1.38
internet_yes 0.76
romantic_yes -1.39
Name: Scaled Coefficients, dtype: float64
Final Comparison#
compare = pd.concat([coeffs_mvp, coeffs_mvp_scaled],axis=1)
compare
| Coefficients | Scaled Coefficients | |
|---|---|---|
| age | -0.34 | -0.44 |
| Medu | 0.58 | 0.63 |
| Fedu | -0.06 | -0.06 |
| traveltime | -0.13 | -0.09 |
| studytime | 0.29 | 0.24 |
| failures | -1.79 | -1.29 |
| famrel | 0.12 | 0.11 |
| freetime | 0.27 | 0.27 |
| goout | -0.70 | -0.78 |
| Dalc | -0.33 | -0.29 |
| Walc | 0.36 | 0.47 |
| health | -0.21 | -0.30 |
| absences | 0.05 | 0.38 |
| school_MS | 0.61 | 0.61 |
| sex_M | 1.00 | 1.00 |
| address_U | 0.60 | 0.60 |
| famsize_LE3 | 0.29 | 0.29 |
| Pstatus_T | -0.12 | -0.12 |
| Mjob_at_home | 2.75 | 1.65 |
| Mjob_health | 4.74 | 3.64 |
| Mjob_other | 2.74 | 1.64 |
| Mjob_services | 3.59 | 2.49 |
| Mjob_teacher | 1.42 | 0.33 |
| Fjob_at_home | 3.21 | 2.12 |
| Fjob_health | 3.34 | 2.24 |
| Fjob_other | 2.23 | 1.13 |
| Fjob_services | 2.39 | 1.30 |
| Fjob_teacher | 4.06 | 2.97 |
| reason_course | 2.82 | 1.45 |
| reason_home | 3.60 | 2.22 |
| reason_other | 4.56 | 3.19 |
| reason_reputation | 4.26 | 2.89 |
| guardian_father | 4.43 | 2.61 |
| guardian_mother | 4.88 | 3.05 |
| guardian_other | 5.93 | 4.10 |
| schoolsup_yes | -1.08 | -1.08 |
| famsup_yes | -1.07 | -1.07 |
| paid_yes | 0.41 | 0.41 |
| activities_yes | 0.06 | 0.06 |
| nursery_yes | -0.13 | -0.13 |
| higher_yes | 1.38 | 1.38 |
| internet_yes | 0.76 | 0.76 |
| romantic_yes | -1.39 | -1.39 |
compare = compare.sort_values('Coefficients')
compare['Diff'] = compare['Scaled Coefficients'] - compare['Coefficients']
compare
| Coefficients | Scaled Coefficients | Diff | |
|---|---|---|---|
| failures | -1.79 | -1.29 | 0.50 |
| romantic_yes | -1.39 | -1.39 | -0.00 |
| schoolsup_yes | -1.08 | -1.08 | 0.00 |
| famsup_yes | -1.07 | -1.07 | -0.00 |
| goout | -0.70 | -0.78 | -0.09 |
| age | -0.34 | -0.44 | -0.10 |
| Dalc | -0.33 | -0.29 | 0.04 |
| health | -0.21 | -0.30 | -0.09 |
| nursery_yes | -0.13 | -0.13 | -0.00 |
| traveltime | -0.13 | -0.09 | 0.03 |
| Pstatus_T | -0.12 | -0.12 | -0.00 |
| Fedu | -0.06 | -0.06 | -0.00 |
| absences | 0.05 | 0.38 | 0.33 |
| activities_yes | 0.06 | 0.06 | 0.00 |
| famrel | 0.12 | 0.11 | -0.01 |
| freetime | 0.27 | 0.27 | 0.00 |
| famsize_LE3 | 0.29 | 0.29 | -0.00 |
| studytime | 0.29 | 0.24 | -0.05 |
| Walc | 0.36 | 0.47 | 0.11 |
| paid_yes | 0.41 | 0.41 | 0.00 |
| Medu | 0.58 | 0.63 | 0.05 |
| address_U | 0.60 | 0.60 | 0.00 |
| school_MS | 0.61 | 0.61 | 0.00 |
| internet_yes | 0.76 | 0.76 | 0.00 |
| sex_M | 1.00 | 1.00 | 0.00 |
| higher_yes | 1.38 | 1.38 | -0.00 |
| Mjob_teacher | 1.42 | 0.33 | -1.10 |
| Fjob_other | 2.23 | 1.13 | -1.10 |
| Fjob_services | 2.39 | 1.30 | -1.10 |
| Mjob_other | 2.74 | 1.64 | -1.10 |
| Mjob_at_home | 2.75 | 1.65 | -1.10 |
| reason_course | 2.82 | 1.45 | -1.37 |
| Fjob_at_home | 3.21 | 2.12 | -1.10 |
| Fjob_health | 3.34 | 2.24 | -1.10 |
| Mjob_services | 3.59 | 2.49 | -1.10 |
| reason_home | 3.60 | 2.22 | -1.37 |
| Fjob_teacher | 4.06 | 2.97 | -1.10 |
| reason_reputation | 4.26 | 2.89 | -1.37 |
| guardian_father | 4.43 | 2.61 | -1.83 |
| reason_other | 4.56 | 3.19 | -1.37 |
| Mjob_health | 4.74 | 3.64 | -1.10 |
| guardian_mother | 4.88 | 3.05 | -1.83 |
| guardian_other | 5.93 | 4.10 | -1.83 |
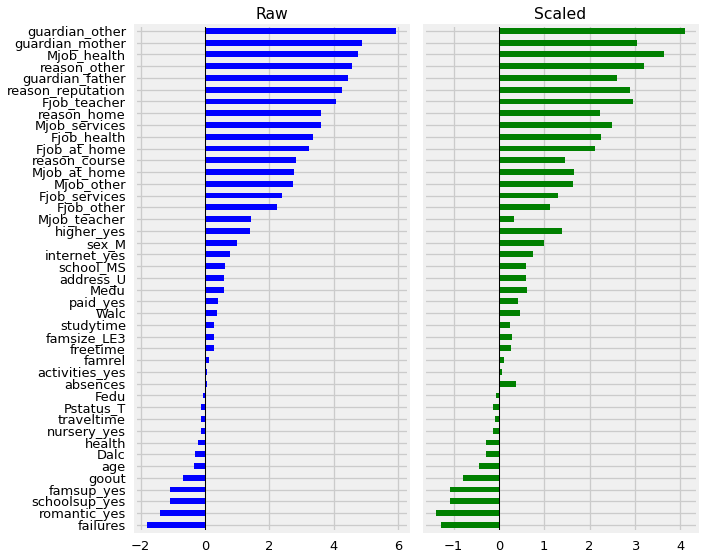
fig, axes = plt.subplots(ncols=2,figsize=(10,8),sharey=True)
compare['Coefficients'].plot(kind='barh',color='blue',ax=axes[0],title="Raw")
compare['Scaled Coefficients'].plot(kind='barh',color='green',ax=axes[1],title='Scaled')
[ax.axvline(0,color='black',lw=1) for ax in axes]
fig.tight_layout()
# ax = coeffs_mvp.sort_values().plot(kind='barh',figsize=(6,10))
# ax.axvline(0,color='k')
# ax.set_title('LinearRegression Coefficients');
Notice how VERY diferent our coefficients are now that we have removed the students’ grades from the prior 2 years!
BOOKMARK: interpret new coeffs
Selecting Our Final Model for Extracting Insights#
Out of all of the variants we have tried, the best one to use going forward is our Ordinal encoded zipcodes with an intercept. (once again, you can make an argument for using the one without an intercept as well).
coeffs_mvp.sort_values()
failures -1.79
romantic_yes -1.39
schoolsup_yes -1.08
famsup_yes -1.07
goout -0.70
age -0.34
Dalc -0.33
health -0.21
nursery_yes -0.13
traveltime -0.13
Pstatus_T -0.12
Fedu -0.06
absences 0.05
activities_yes 0.06
famrel 0.12
freetime 0.27
famsize_LE3 0.29
studytime 0.29
Walc 0.36
paid_yes 0.41
Medu 0.58
address_U 0.60
school_MS 0.61
internet_yes 0.76
sex_M 1.00
higher_yes 1.38
Mjob_teacher 1.42
Fjob_other 2.23
Fjob_services 2.39
Mjob_other 2.74
Mjob_at_home 2.75
reason_course 2.82
Fjob_at_home 3.21
Fjob_health 3.34
Mjob_services 3.59
reason_home 3.60
Fjob_teacher 4.06
reason_reputation 4.26
guardian_father 4.43
reason_other 4.56
Mjob_health 4.74
guardian_mother 4.88
guardian_other 5.93
Name: Coefficients, dtype: float64
In the next lesson, we will focus on another type of model-based values.

